Define a Set of Multivariate Multidimensional Functional Data objects

The `mvmfd` class represents functional data ...

Constructor for `mvmfd` objects (same as `Mvmfd`)

Usage

Mvmfd(...)

Arguments

...

A `mfd` objects which have separated by comma

See also

mvbasismfd, mfd

Active bindings

basis

A `mvbasismfd` object

coefs

a matrix of the coefficients.

nobs

number of observation

nvar

number of variables

Methods

Public methods

• mvmfd$new()

• mvmfd$eval()

• mvmfd$print()

• mvmfd$clone()

---

Method new()

Constructor for `mvmfd` objects (same as 'Mvmfd')

Usage

mvmfd$new(...)

Arguments

...

A `mfd` objects which have separated by comma

---

Method eval()

Eval method for `mvmfd` objects

Usage

mvmfd$eval(evalarg)

Arguments

evalarg

A list of numeric vectors of argument values at which the `mvmfd` is to be evaluated.

Returns

A list of evaluated values

---

Method print()

Print method for `mvmfd` objects

Usage

mvmfd$print(...)

Arguments

...

Additional arguments to be passed to `print`

---

Method clone()

The objects of this class are cloneable with this method.

Usage

mvmfd$clone(deep = FALSE)

Arguments

deep

Whether to make a deep clone.

Examples

require(fda)
bs1 <- create.fourier.basis(c(0, 2 * pi), 5)
bs2 <- create.bspline.basis(c(0, 1), 7)
bs3 <- create.exponential.basis(c(0, 2), 3)
nobs <- 10
argval1 <- seq(0, 2 * pi, length.out = 12)
X1 <- outer(sin(argval1), seq(0.5, 1.5, length.out = nobs))
mdbs1 <- Basismfd(bs1)
mfd1 <- Mfd(argval1, X1, mdbs1)
mdbs2 <- Basismfd(bs1)
argval2 <- argval1
X2 <- outer(cos(argval2), seq(0.2, 1.5, length.out = nobs))
mfd2 <- Mfd(argval2, X2, mdbs1)
mvmfd1 <- Mvmfd(mfd1, mfd2)
mvmfd1[1]
#> A 'mvmfd' object with 2 variable(s):
#> 
#> Variable 1:
#> A 1-Dimensional 'mfd' object:
#> nobs: 1 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
#> 
#> Variable 2:
#> A 1-Dimensional 'mfd' object:
#> nobs: 1 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
mvmfd1[1, 1]
#> A 1-Dimensional 'mfd' object:
#> nobs: 1 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
mvmfd1[1:5, 2]
#> A 1-Dimensional 'mfd' object:
#> nobs: 5 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
mvmfd1[, 1]
#> A 1-Dimensional 'mfd' object:
#> nobs: 10 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
mvmfd1[1:5, ]
#> A 'mvmfd' object with 2 variable(s):
#> 
#> Variable 1:
#> A 1-Dimensional 'mfd' object:
#> nobs: 5 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
#> 
#> Variable 2:
#> A 1-Dimensional 'mfd' object:
#> nobs: 5 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
evalarg <- list(argval1, argval2)
mvmfd1$eval(evalarg)
#> [[1]]
#>                [,1]          [,2]          [,3]          [,4]          [,5]
#>  [1,]  1.175889e-17 -5.566336e-17 -5.989427e-17 -8.533914e-18  4.282644e-17
#>  [2,]  2.703204e-01  3.303916e-01  3.904628e-01  4.505340e-01  5.106052e-01
#>  [3,]  4.548160e-01  5.558862e-01  6.569564e-01  7.580267e-01  8.590969e-01
#>  [4,]  4.949107e-01  6.048909e-01  7.148710e-01  8.248512e-01  9.348314e-01
#>  [5,]  3.778748e-01  4.618470e-01  5.458191e-01  6.297913e-01  7.137635e-01
#>  [6,]  1.408663e-01  1.721699e-01  2.034735e-01  2.347771e-01  2.660807e-01
#>  [7,] -1.408663e-01 -1.721699e-01 -2.034735e-01 -2.347771e-01 -2.660807e-01
#>  [8,] -3.778748e-01 -4.618470e-01 -5.458191e-01 -6.297913e-01 -7.137635e-01
#>  [9,] -4.949107e-01 -6.048909e-01 -7.148710e-01 -8.248512e-01 -9.348314e-01
#> [10,] -4.548160e-01 -5.558862e-01 -6.569564e-01 -7.580267e-01 -8.590969e-01
#> [11,] -2.703204e-01 -3.303916e-01 -3.904628e-01 -4.505340e-01 -5.106052e-01
#> [12,] -1.107058e-16 -2.053424e-16 -2.367877e-16 -2.126417e-16 -1.884957e-16
#>                [,6]          [,7]          [,8]          [,9]         [,10]
#>  [1,] -8.600566e-18 -8.939168e-17  2.572277e-17 -1.368147e-17 -1.293677e-16
#>  [2,]  5.706764e-01  6.307476e-01  6.908188e-01  7.508900e-01  8.109612e-01
#>  [3,]  9.601671e-01  1.061237e+00  1.162308e+00  1.263378e+00  1.364448e+00
#>  [4,]  1.044812e+00  1.154792e+00  1.264772e+00  1.374752e+00  1.484732e+00
#>  [5,]  7.977357e-01  8.817078e-01  9.656800e-01  1.049652e+00  1.133624e+00
#>  [6,]  2.973844e-01  3.286880e-01  3.599916e-01  3.912952e-01  4.225988e-01
#>  [7,] -2.973844e-01 -3.286880e-01 -3.599916e-01 -3.912952e-01 -4.225988e-01
#>  [8,] -7.977357e-01 -8.817078e-01 -9.656800e-01 -1.049652e+00 -1.133624e+00
#>  [9,] -1.044812e+00 -1.154792e+00 -1.264772e+00 -1.374752e+00 -1.484732e+00
#> [10,] -9.601671e-01 -1.061237e+00 -1.162308e+00 -1.263378e+00 -1.364448e+00
#> [11,] -5.706764e-01 -6.307476e-01 -6.908188e-01 -7.508900e-01 -8.109612e-01
#> [12,] -2.671371e-16 -3.751426e-16 -2.872425e-16 -3.538611e-16 -4.967617e-16
#> 
#> [[2]]
#>              [,1]        [,2]        [,3]        [,4]       [,5]       [,6]
#>  [1,]  0.20000000  0.34444444  0.48888889  0.63333333  0.7777778  0.9222222
#>  [2,]  0.16825071  0.28976511  0.41127950  0.53279390  0.6543083  0.7758227
#>  [3,]  0.08308300  0.14308739  0.20309178  0.26309617  0.3231006  0.3831050
#>  [4,] -0.02846297 -0.04901956 -0.06957614 -0.09013273 -0.1106893 -0.1312459
#>  [5,] -0.13097215 -0.22556314 -0.32015414 -0.41474513 -0.5093361 -0.6039271
#>  [6,] -0.19189859 -0.33049202 -0.46908545 -0.60767888 -0.7462723 -0.8848657
#>  [7,] -0.19189859 -0.33049202 -0.46908545 -0.60767888 -0.7462723 -0.8848657
#>  [8,] -0.13097215 -0.22556314 -0.32015414 -0.41474513 -0.5093361 -0.6039271
#>  [9,] -0.02846297 -0.04901956 -0.06957614 -0.09013273 -0.1106893 -0.1312459
#> [10,]  0.08308300  0.14308739  0.20309178  0.26309617  0.3231006  0.3831050
#> [11,]  0.16825071  0.28976511  0.41127950  0.53279390  0.6543083  0.7758227
#> [12,]  0.20000000  0.34444444  0.48888889  0.63333333  0.7777778  0.9222222
#>             [,7]       [,8]       [,9]      [,10]
#>  [1,]  1.0666667  1.2111111  1.3555556  1.5000000
#>  [2,]  0.8973371  1.0188515  1.1403659  1.2618803
#>  [3,]  0.4431093  0.5031137  0.5631181  0.6231225
#>  [4,] -0.1518025 -0.1723591 -0.1929157 -0.2134723
#>  [5,] -0.6985181 -0.7931091 -0.8877001 -0.9822911
#>  [6,] -1.0234592 -1.1620526 -1.3006460 -1.4392395
#>  [7,] -1.0234592 -1.1620526 -1.3006460 -1.4392395
#>  [8,] -0.6985181 -0.7931091 -0.8877001 -0.9822911
#>  [9,] -0.1518025 -0.1723591 -0.1929157 -0.2134723
#> [10,]  0.4431093  0.5031137  0.5631181  0.6231225
#> [11,]  0.8973371  1.0188515  1.1403659  1.2618803
#> [12,]  1.0666667  1.2111111  1.3555556  1.5000000
#> 
mvmfd1 + mvmfd1
#> A 'mvmfd' object with 2 variable(s):
#> 
#> Variable 1:
#> A 1-Dimensional 'mfd' object:
#> nobs: 10 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
#> 
#> Variable 2:
#> A 1-Dimensional 'mfd' object:
#> nobs: 10 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
mean(mvmfd1)
#> A 'mvmfd' object with 2 variable(s):
#> 
#> Variable 1:
#> A 1-Dimensional 'mfd' object:
#> nobs: 1 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
#> 
#> Variable 2:
#> A 1-Dimensional 'mfd' object:
#> nobs: 1 
#> basis 1:
#> type: fourier
#> nbasis: 5
#> support: 0 6.283185 
inprod_mvmfd(mvmfd1, mvmfd1)
#>           [,1]     [,2]     [,3]     [,4]     [,5]     [,6]      [,7]      [,8]
#>  [1,] 0.911061 1.176351 1.441641 1.706931 1.972221 2.237511  2.502801  2.768090
#>  [2,] 1.176351 1.545973 1.915595 2.285217 2.654838 3.024460  3.394082  3.763704
#>  [3,] 1.441641 1.915595 2.389548 2.863502 3.337456 3.811410  4.285364  4.759318
#>  [4,] 1.706931 2.285217 2.863502 3.441788 4.020074 4.598360  5.176645  5.754931
#>  [5,] 1.972221 2.654838 3.337456 4.020074 4.702691 5.385309  6.067927  6.750545
#>  [6,] 2.237511 3.024460 3.811410 4.598360 5.385309 6.172259  6.959208  7.746158
#>  [7,] 2.502801 3.394082 4.285364 5.176645 6.067927 6.959208  7.850490  8.741772
#>  [8,] 2.768090 3.763704 4.759318 5.754931 6.750545 7.746158  8.741772  9.737385
#>  [9,] 3.033380 4.133326 5.233271 6.333217 7.433162 8.533108  9.633053 10.732999
#> [10,] 3.298670 4.502948 5.707225 6.911503 8.115780 9.320057 10.524335 11.728612
#>            [,9]     [,10]
#>  [1,]  3.033380  3.298670
#>  [2,]  4.133326  4.502948
#>  [3,]  5.233271  5.707225
#>  [4,]  6.333217  6.911503
#>  [5,]  7.433162  8.115780
#>  [6,]  8.533108  9.320057
#>  [7,]  9.633053 10.524335
#>  [8,] 10.732999 11.728612
#>  [9,] 11.832944 12.932890
#> [10,] 12.932890 14.137167
norm_mvmfd(mvmfd1)
#>  [1] 0.9544951 1.2433715 1.5458164 1.8552057 2.1685690 2.4844031 2.8018726
#>  [8] 3.1204783 3.4399047 3.7599424
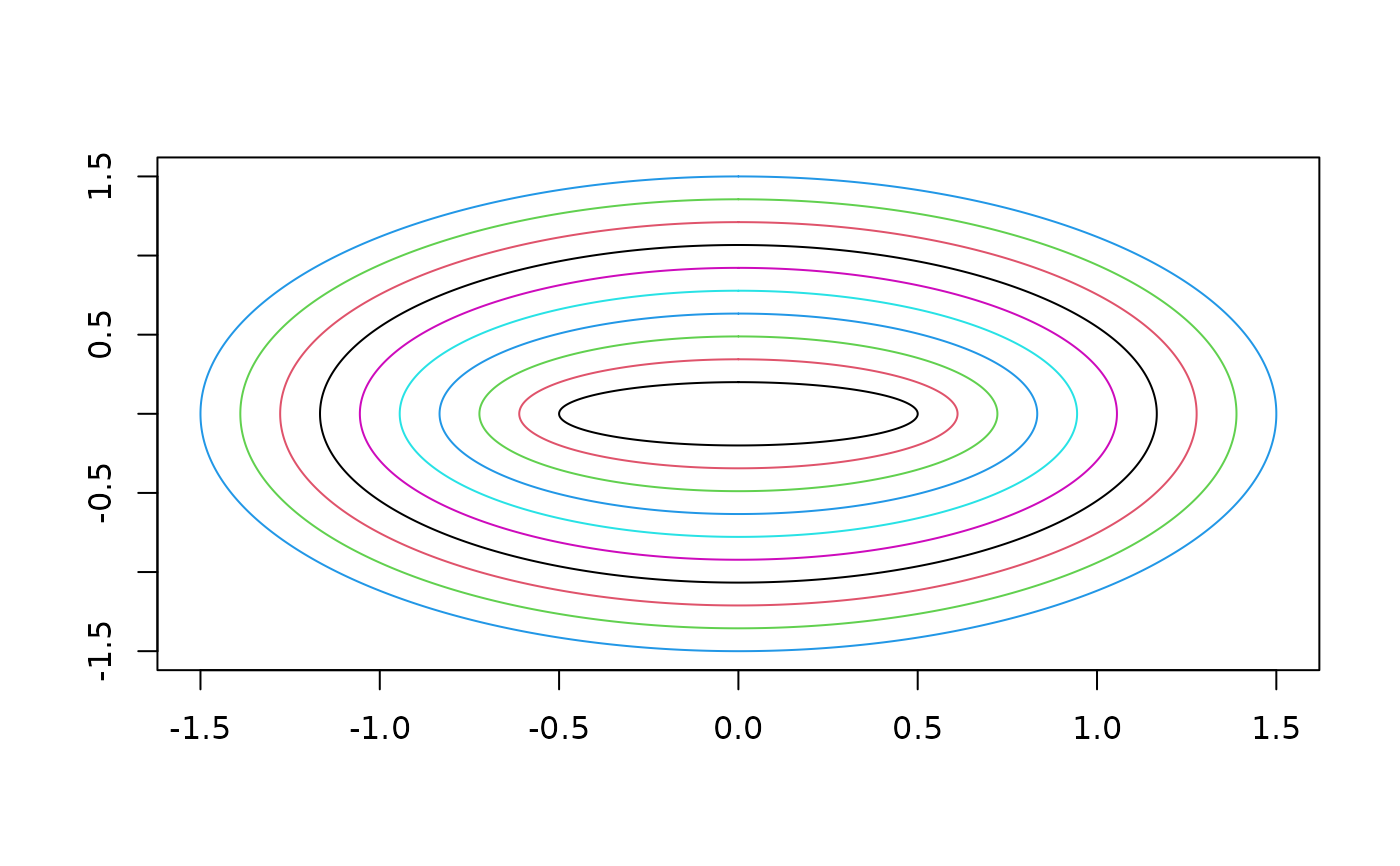
plot(mvmfd1)

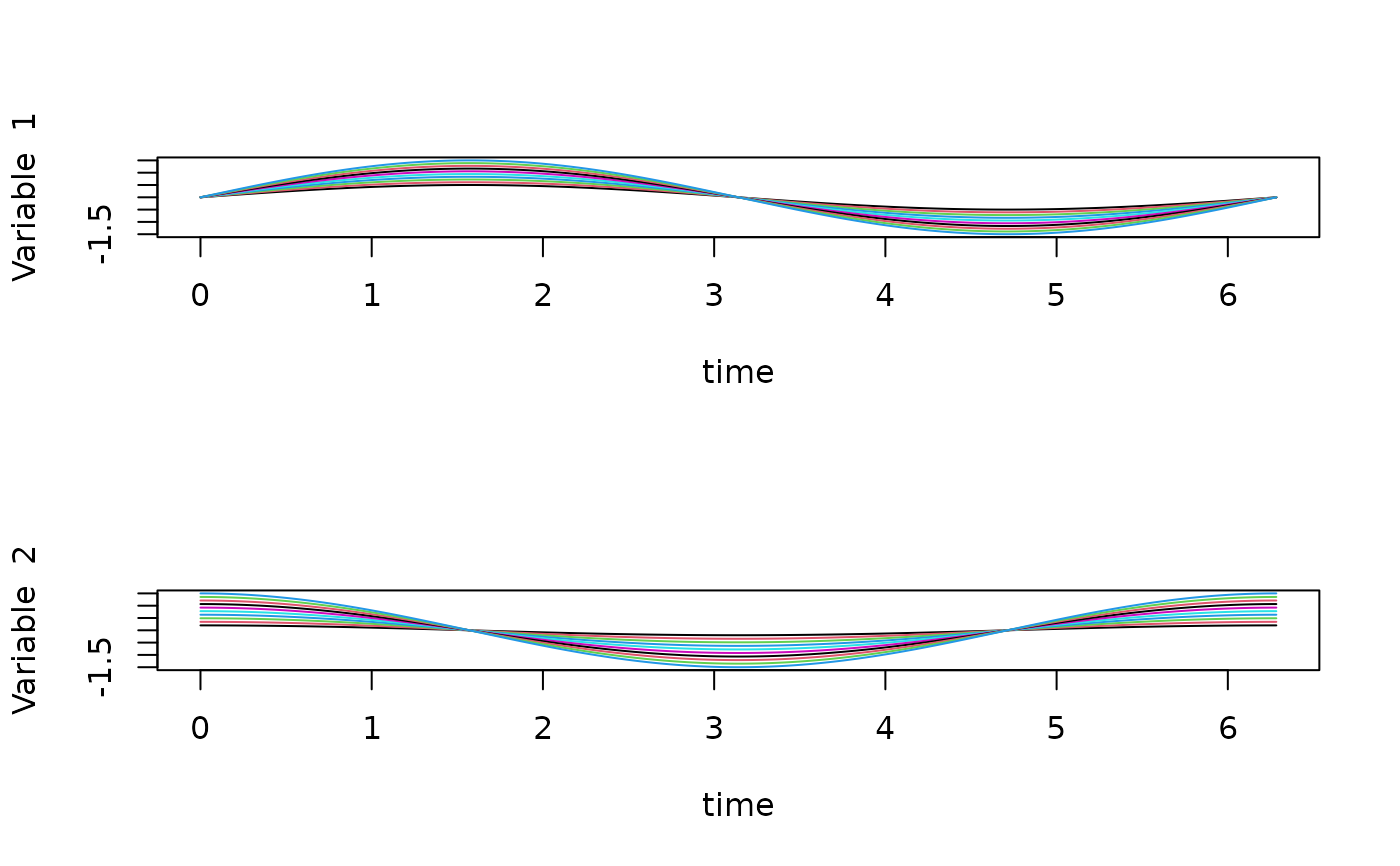bimfdplot(mvmfd1)